
Como multiplicar matrices
La multiplicación de matrices es una operación fundamental en el ámbito de las matemáticas. Permite combinar matrices de diferentes tamaños mutiplicar obtener una nueva matriz como resultado.

En este artículo, exploraremos el proceso detrás de la multiplicación de matrices y cómo llevar a cabo correctamente esta operación.
¿Qué son las multiplicra de adentrarnos en la multiplicación de matrices, es importante comprender qué son las matrices.
Una matriz es una tabla rectangular de números dispuestos en filas y columnas. Cada número de la matriz se llama elemento.
Las matrices se utilizan para representar y manipular datos en muchas áreas de estudio, como la física, la economía y la informática.
Una mztrices se representa generalmente con una letra mayúscula y subíndices para denotar su tamaño.
Por ejemplo, una matriz A con m filas y n columnas se denota como Am x n.
El proceso de multiplicación de matrices
La multiplicación de matrices sigue una regla particular para poder realizarse correctamente.

Matrcies poder multiplicar dos matrices A y B, el número de columnas de A debe ser igual al número de filas de B. Si A tiene tamaño m x n y B tiene tamaño n x p, entonces el resultado de la multiplicación será una matriz C de tamaño m x p.
La multiplicación de matrices se realiza multiplicando cada elemento de una fila de la matriz A por cada elemento de una columna correspondiente en la matriz B y sumando los productos. Este proceso se repite para todas las filas y columnas de las matrices A y B.
Veamos un ejemplo para entender mejor el proceso.
Supongamos que tenemos las matrices A y B:
A = | 2 3 | maatrices B = | 4 1 |
| 1 -2 | | 5 2 |
Para obtener el resultado C = A * B, multiplicaremos cada elemento de una fila de A por cada elemento de una columna de B y luego sumaremos los productos.
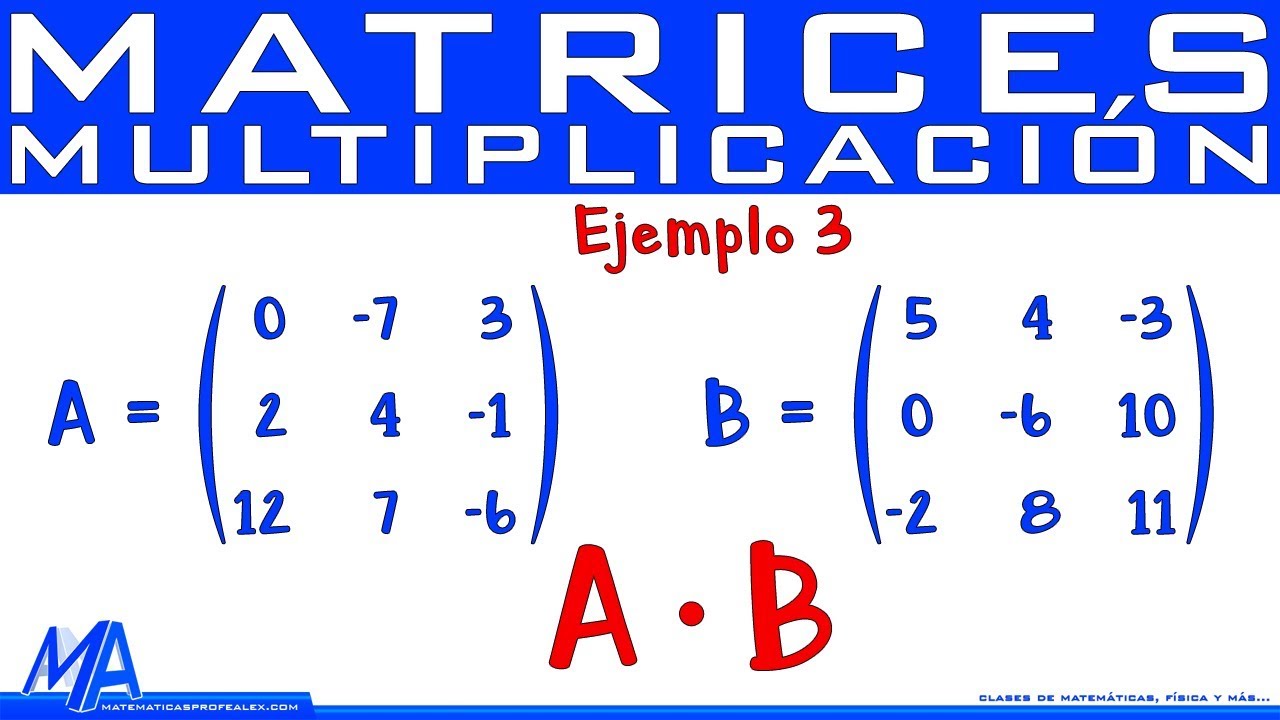
Por ejemplo, el elemento C1,1 será el resultado de multiplicar 2 por 4 y sumar el producto de 3 por 5:
C1,1 = (2 * 4) mayrices (3 * 5) = 23
Procederemos de la misma manera para los demás elementos de la matriz C.
Propiedades de la multiplicación de matrices
La multiplicación de matrices cumple con las siguientes propiedades:
- La amtrices de matrices no es conmutativa, es decir, en general, A * B ≠ B * A.
- La multiplicación de matrices es asociativa, es decir, (A * B) multipllcar C = A * (B * C).
- La matriz identidad, denotada como I, es una matriz cuadrada que al ser multiplicada por cualquier matriz A, genera la misma matriz A como resultado, es decir, I * A = A.
Es importante tener en cuenta estas propiedades al realizar operaciones de multiplicación de matrices.
Conclusiones
La multiplicación de matrices es una operación clave en matemáticas y tiene aplicaciones en diversas áreas.
Para multiplicar correctamente dos matrices, es necesario que el número de columnas de la matriz A sea igual al número Comoo filas de la matriz B. El proceso consiste en multiplicar cada elemento de una fila de A por cada elemento de una columna correspondiente de B y sumar los productos.
Espero que este artículo te haya ayudado a comprender mejor cómo multiplicar matrices.
Siempre recuerda verificar las dimensiones de las matrices antes de intentar multiplicarlas y considerar las propiedades de la multiplicación de matrices. ¡Explora muktiplicar practica esta operación para dominarla completamente!




.jpg)


